Hash 是一种很神奇的数据结构
HashTable
HashTable 散列表 哈希表: 是一种数据结构,它提供快速的插入和查找操作,不管表中有多少数据,插入删除和查找的时间都接近O(1)
**优点:**HashTable其实是基于数组的,所以在查询方面非常的快,同时它不像普通数组那样紧密排列,在数值未满的时候所有的值其实是散部在数组中的某个位置上的,所以在插入和删除的时候不用像普通数组一样让余下的值一个个的挪。
**缺点:**同时也因为它的基于数组的,所以创建以后难以扩展,当HashTable被基本填满的时候,性能严重下降,而且不能顺序遍历。
一个输入传进来的时候会经过散列函数,计算出一个值,这个值就是这个输入在HashTable中的位置,称为HashCode 哈希值 散列值。
当HashTable中的值还不多的时候各种操作的效率是非常高的,但是HashTable快满的时候各种操作的效率就开始变低了
开放寻址法
线性探测方法
比如一个HashTable的长度是8,现在只剩下 ~6~ 这个位置是空的
而一个输入经过散列函数计算之后得到的结果是 ~7~ ,一看 ~7~ 上面有人占了,怎么办呢?
往下找空位咯,~7~ 下面是 ~0~ ,有人了,下一个 ~1~ ,有人了,下一个 ~2~ ,有人了…下一个 ~6~ ,耶没人,上去!
这样几乎遍历了一整个数组,效率是非常低的,HashTable小的时候还能忍受,如果HashTable长度是2000呢?20000呢?
上述的方法其实就是当散列函数计算出来的值上面已经有值的时候的解决方法之一,开放寻址法中的线性探测,往下找空位,找到进填进去。最坏的情况下就是几乎遍历整个数组。
二次探测方法
另一种的思路有那么点像二分查找法,叫做二次探测方法
比如表中只有 ~3~ 是有空位的,其余都是满的
而一个输入经过散列函数计算之后得到的结果是 ~7~,一看 ~7~ 上面有人了,怎么办呢?
CurrentCode + 0,CurrentCode + 1^2^ ,CurrentCode - 1 ^2^,CurrentCode + 2^2^,CurrentCode - 2^2^,……
7不行就 + 1^2^ = 8,8还是不行,那就7 - 1^2^ = 6,6还是不行,那就7 - 2^2^ = 3,3可以,上去!
因为进行试探的步长都是二次方,所以叫 二次探测方法
双重散列方法
还有一种方法叫做 双重散列方法
就是使用第一个哈希函数计算的值如果被占用了,就找第二个哈希函数,直到找到空闲的存储位置
不管用那种方法,只要HashTable空位不多的时候散列冲突的概率就会大大提高,尽可能保证HashTable中有一定比例的空位。
一般用加载因子来表示空位的多少。加载因子越大表示约满,反之亦然。
链表法
HashTable中每个元素对应一条链表,所有散列值相同的元素放到相同的链表中。如下图
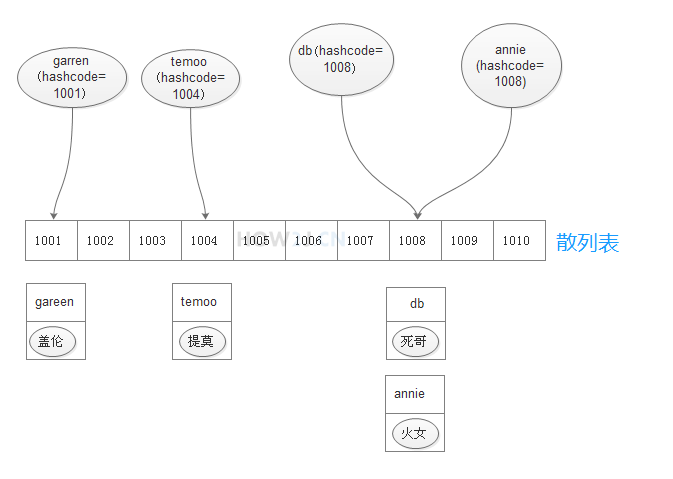
查找的时候先通过HashCode找到位置,然后将值与链表中的值逐个使用 equals() 对比。
But
但其实HashTable是元素数量不能超过总容量的一半,当HashTable太满的时候,一个选择是扩容数组,创建一个新的容量为 CurrentCapacity * 1.34 + n = 2^m 的数组,把值放到新数组,但是元素的索引没法复制,会被重新哈希化。
$$
CurrentCapacity * 1.34 + n = 2^m = NewCapacity
$$
举个栗子
一本字典有1000页,当你要查找Link这个词的时候,肯定想去翻目录,目录显示在第666页,那么你是不是可以直接翻到666页找这个单词?也就是所Link这个单词在散列表[666],但是第666页可能不止这一个单词哦,那你是不是要一个一个进行equals才能知道是哪个呢?因为知道在哪一条链表上,所以尽管遍历看起来很慢,但总比遍历所有链表快吧?