怎么和聊天才能不被人看到信息内容?
加密与解密
应用场景:通信
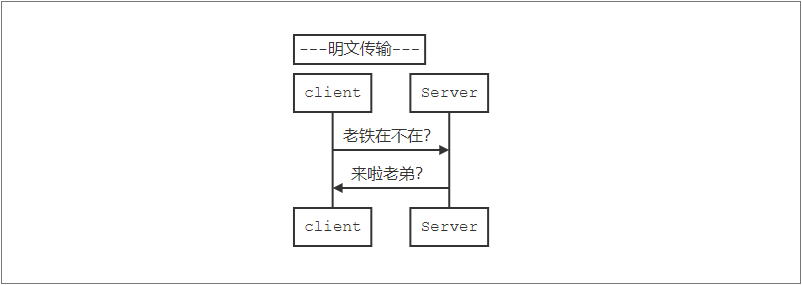
传统的通信场景:明文
>_
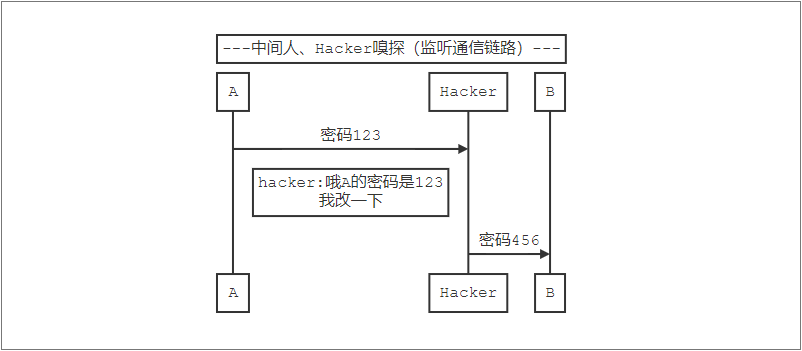
如果这时候有个Hacker在中间嗅探他们的通信链路,那他们的内容就全都被看到了,甚至会被篡改
>_
加密&解密
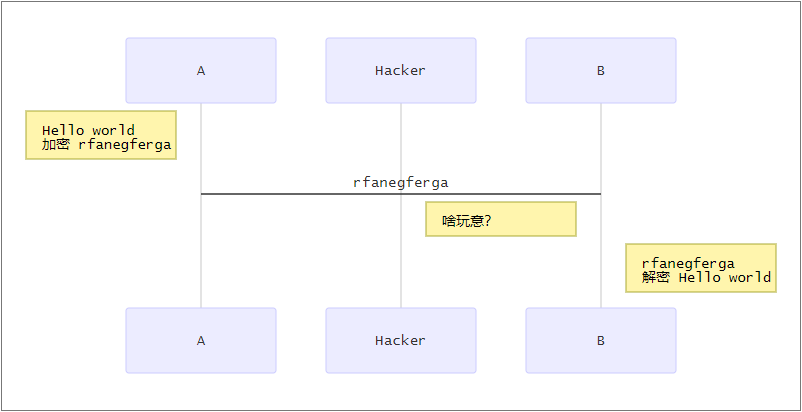
明文有问题,那就加密,让中间的Hacker看不懂
凯撒密码
通过约定的偏移和回正,达到A、B都看得懂,中间人看不懂的目的
加密:A发送的信息,全部右偏移3个字母
解密:B接收后左回正3个字母,就得到正确信息了。
例如:Hello world
右偏移后变成 Khnnr zrung
但是这样的加密太容易被破解了。凯撒密码是一种很古老的在战争中使用过的一种加密信件的方式,这里不说汉字,就说英文26个字母,最多进行(回正1,回正2,回正3…回正25,回正-1,回正-2…回正-25)共50次就可以破解。
对称加密
A、B都将信息异或运算
如果将信息转成二进制,然后和另一个二进制(这里用E表示),得到加密结果
那加密结果和E异或就能得到原本的信息的二进制,再转换成文字就得到了信息。
A ^ E = C C ^ E = A
例如:
加密的一方
假设 Hello world 的二进制是 0110 0101 1101
E 是: 0101 1001 1010
加密(异或)的结果就是: 0011 1100 0111
解密的一方
收到了加密的信息: 0011 1100 0111
E 是: 0101 1001 1010
解密(异或)的结果就是:0110 0101 1101
>_
这就是利用异或的特性来进行信息的加密。所以关键的E 就叫做密钥(所以拿到密钥就能破解了)。
要确保双方都有 E 这把密钥。
对称加密有3个特点:
- 仅做XOR(异或)运算,速度快 –优点
- 密钥跟数据长度相等 –缺点
- 双方需要提前拥有密钥
加密分片
对称加密的缺点也明显,密钥长度跟数据长度相等。
解决的办法是:
把信息分组,每组对应一段密钥,分别做异或运算就可以得到密文分片,再合并到一起就得到密文(加密的信息)了。
接收的一方分别做异或运算得到明文分片,在合并到一起就得到原本的信息了。
加密分片的特点:
- 数据按密钥长度分组,不足的填充
- 可以并行计算各个分组,优化了性能
- 密文跟明文的序列存在规律对应关系
上面说的就是DES的ECB模式加密
不过这种简单的分组模式也是很容易发现规律
一般的改进思路是:信息第一次分组、加密、合并得到了一次密文,然后再进行第二次分组、加密、合并得到二次密文。
或者第一次分组,一次加密、二次加密、合并。
非对称加密
请求方请求公钥,接收方发送公钥,请求方加密后发送,接收方用私钥解密
那密钥这么好,但是有个问题:E(密钥)怎么传输?明文还是密文?
答案是:明文。
那密钥是明文的,被Hacker嗅探到了,那上面那些不都白费了。
所以就有了 非对称加密
>_

简单说就是:我先要个保险箱,然后把密钥放进去,关上。这个保险箱只有你开的了,所以被Hacker截获了他也开不了。
这就是非对称加密。谁都可以跟B拿保险箱,只有B自己才开得了保险箱。
| |
他们的特点就是:
- 任何人都可以请求并拿到公钥
- 用公钥加密明文变成密文
- 仅能用私钥解开密文得到明文
- 私钥不能丢失
RSA就是这样一个公钥(保险箱)私钥(钥匙)的算法,具体的数学应用利用了 大质数相乘难以分解,费马小定理 等数学理论,使得它难以破解(思考:所以从质数、小定理这些数学理论入手,是不是有机会破解非对称加密?)。
非对称加密需要做乘法模除等运算,性能效率比对称加密差很多。
对称加密需要做异或预算,性能效率比较高。
那么就综合起来,用非对称加密传输密钥E,然后再用对称加密传输数据。
认证
找个我们都信得过的组织来保证我们不会被骗走密钥
接上面的思考,其实不用那么麻烦,硬刚刚不赢,可以曲线救国嘛~~
>_
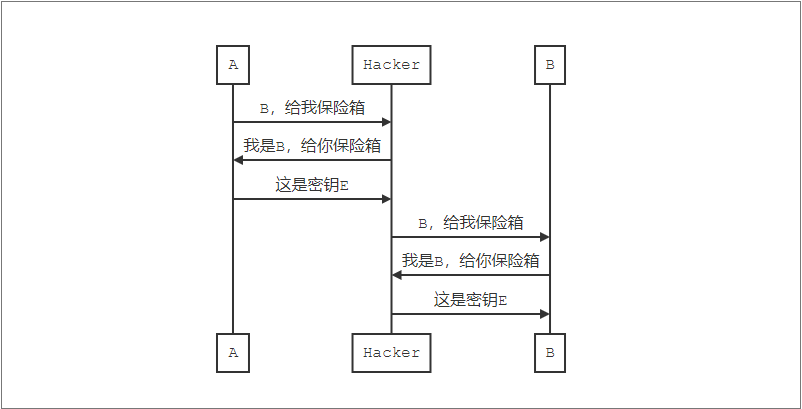
如上,因为Hacker在中间截胡,所以他两边欺骗,然后只是做一个转发的工作。这个过程中,信息就给他看完了,而A、B都以为自己在跟对方通信,其实都被Hacker欺骗了。接下来开始传输数据的时候,Hacker前面拿到了密钥,所以他能解密任何数据,这样就绕过了非对称加密,保险箱不起作用了。
CA证书
那要怎么保证A请求B的公钥(保险箱)后,对方发过来的公钥(保险箱)就一定是B的呢?
这里就需要一个彼此信任的组织,给每个人发身份证。就好像我们信任政府发的个人身份证(假设身份证没法伪造),所以我们看到个人身份证的时候就相信这个叫身份证上的名字。
在加密中,这个政府就是CA,身份证就是CA证书、CA数字签名。
大家都信任CA,所以检查CA证书后我们就相信B 是 B。
这个证书里面有两个重要的内容:B的公钥+CA做的数字签名
CA证书是反过来的,用私钥加密,用公钥解密。
CA用自己的私钥加密B的信息,A手里都有CA的公钥,在收到信息的时候,用CA的公钥解密,如果能解开,就证明B就是B。
换句话说,A请求B发保险箱过来,B先把保险箱给CA做个记号(CA认证加密),然后再发给A,A收到后看看记号跟CA约定的一不一样(CA的公钥解不解得开),如果Hacker发一个自己的保险箱,上面是没记号的(或者记号跟约定的不一样),那就说明这个保险箱是假的。
>_
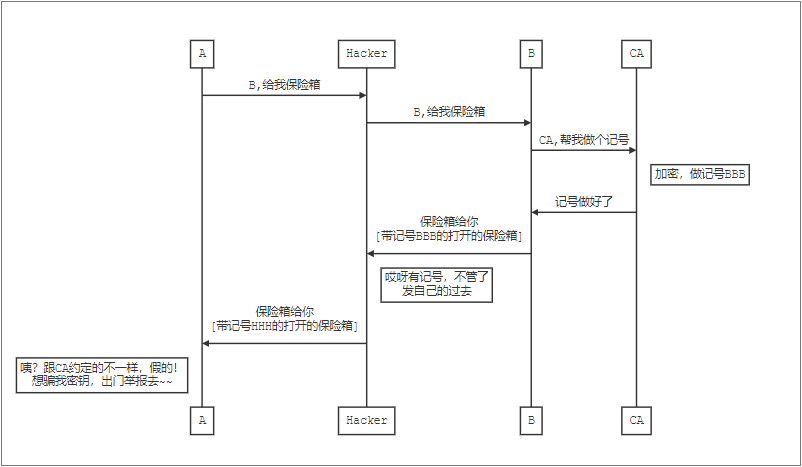
以上就是一个简单的过程,Hacker发的假保险箱(公钥)跟CA约定的不一样(CA公钥解不开),A就停止发送密钥,Hacker欺骗失败
完整性
非对称加密 和 认证 解决了保密性和真实性,但是完整性还没有一个保障。
如果Hacker等A、B非对称加密传输完密钥之后,在对称加密传输数据这个环节入手,篡改信息怎么办?
答案是:哈希一下
单向哈希(Hash)可以把一个输入变成一个定长的输出串,它的特点就是无法从这个输入逆向还原输入内容,并且输入只要有一点改变,哪怕是那么一丢丢,输出串都会完全不同。
>_
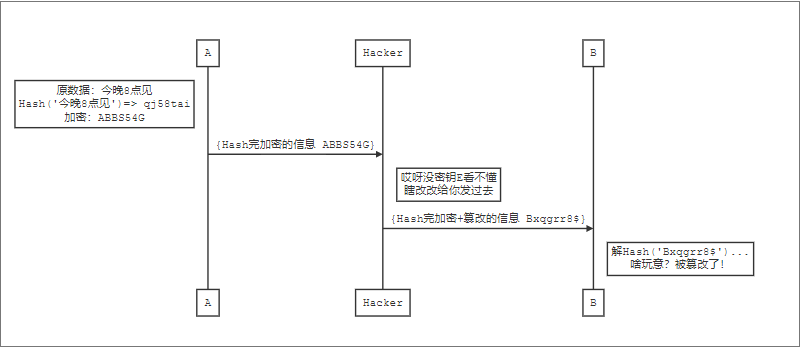
这里哈希并不是这么简单,只需要知道哈希不可逆,一点点改变都会导致结果完全不同。
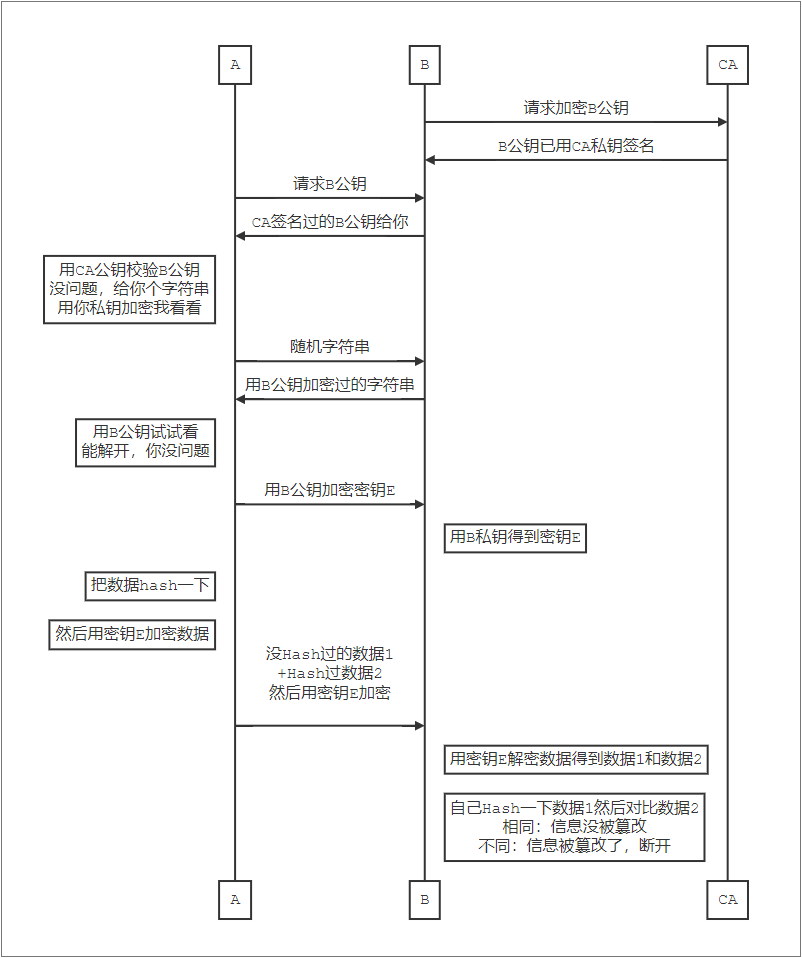
总结
安全可靠的通信:
- B让CA用 # CA私钥 # 签名 [B的公钥](给B的保险箱做个记号)
- A请求B给 [B的公钥](打开的保险箱)
- B发送签名过的 [[B的公钥]](带记号的保险箱)给A
- A用 ## CA的公钥 ## 校验B发来的 [[ B的公钥 ]](检查记号)
- 用 [ B的公钥 ] 加密 “密钥E”(密钥放进保险箱关上门)
- B用【B的私钥】解密 “密钥E”
- A 用 “密钥E” 加密后传输数据
- B 用 “密钥E” 解密数据
>_